Linear Programming and Generator Economics
Using Linear Programming to Minimize Generator Bid Costs
Linear Programming is used in power market economics and operations to minimize the cost of generator providers while considering constraints such as minimum up-time, bands, min/max mw, capability curves, etc.
My simple project example considers the market economics of two generators using linear programming to minimize costs with respect to constraints.
Variables
There are 8 variables in my generator model problem: x1, x2, x3, x4, x5, x6, x7,x8. They are defined as given below:
| Variable | Definition |
| x1 | G1 Bidding Quantity 20 MW Step |
| x2 | G1 Bidding Quantity 30 MW Step |
| x3 | G1 Bidding Quantity 15 MW Step |
| x4 | G1 = x1 + x2 + x3 or total MW to be bid by G1 |
| x5 | G2 Bidding Quantity 18 MW Step |
| x6 | G2 Bidding Quantity 26 MW Step |
| x7 | G2 Bidding Quantity 32 MW Step |
| x8 | G2 = x5 + x6 + x7 or total MW to be bid by G2 |
Objective Function:
The objective of the problem is to minimize cost of combined bids of both generators.
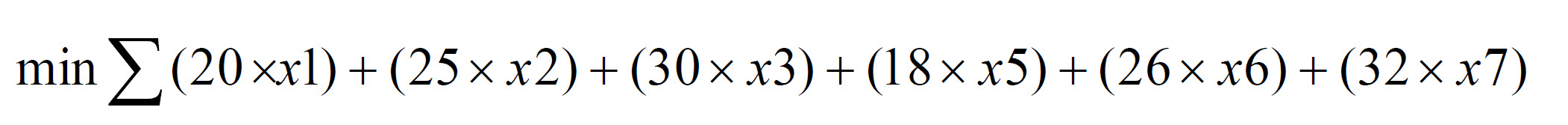
mathematical objective function
The objective function is the sum of the unit price of the MW multiplied by the quantity to be bid added to the other bid ranges and their respective products.
Note: In the MATLAB portion of the model, the x4 and x8 variables are set equal to 0 since it is not in the problem definition to minimize these.
Constraints
The constraints of the problem are shown below:
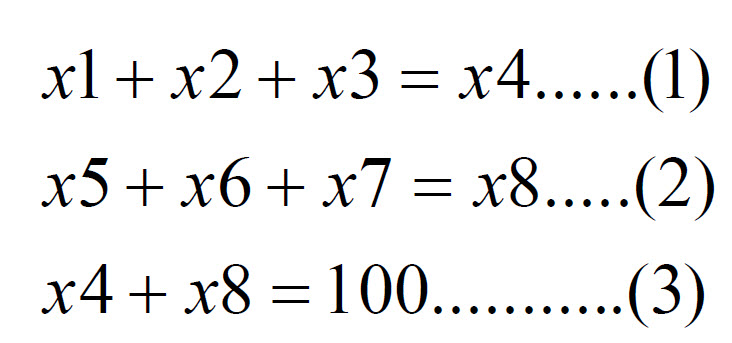
mathematical constraints
Constraint (1) is formulated on the definition that the Generator G1 bids from the given three quantities 20MW, 30MW, or 15 MW. Constraint (2) is formulated on the definition that Generator G2 bids from the given three quantities 15MW, 40MW, or 25MW.
Bounds
The bounds of the model are defined in the problem statement and are shown below:
| Variable | Lower Bound | Upper Bound |
| x1 | 0 | 20 |
| x2 | 0 | 30 |
| x3 | 0 | 15 |
| x4 | 15 | 65 |
| x5 | 0 | 15 |
| x6 | 0 | 40 |
| x7 | 0 | 25 |
| x8 | 10 | 80 |
Optimal Solution
Accepted Quantity
The accepted quantity from each generator range is shown below and in the MATLAB results (attached code):
G1 Bidding Information
| Quantity (MW) | Price ($/MWH) |
| 20 | 20 |
| 30 | 25 |
| 0 | 30 |
G2 Bidding Information
| Quantity (MW) | Price ($/MWH) |
| 15 | 18 |
| 35 | 26 |
| 0 | 32 |
Cost to Supply Load
The minimized cost under the optimal model to supply 100 MW load is $2,330.00. The cost to supply load by generator G1 will be $1150 from G2, $1180.
My Solution Code
You can view and download the GitHub repository here.
You can also download a zip archive of the project code here.
