Security-Constrained Unit Commitment Programming Project
Submitted for graduate course Power Market Operations – May 9th, 2005
Abstract
This paper discusses the security-constrained unit commitment programming project guidelines, formulations, high-level and low-level programming, and procedures to complete a secure and economical system model. Low-level programming was completed for the unit commitment portion. In lieu of security program, a high-level process flow will show security based constraints due to the author’s own constraints discussed in the comments section of the report.
Introduction
Security-Constrained Unit Commitment (SCUC) consists of two components, system security, and economic dispatch. The objective of the problem is focused solely on the economic dispatch of generators with bidding segments, no load costs, starting costs, and other costs incurred during operation. Least cost is desired according to the system operators. Simple economics dictates that generators can supply (X) MW of power at location xyz and deliver the power through the transmission lines L123. However, this is not such a simple problem of who can “bid the lowest price” and win the contract in a short period of time. Location, transmission design, and the generator’s operating efficiencies are conglomerated together to form a complex set of questions that the system operators must answer using analysis before awarding contracts to independent power producers. Thus, much planning and analysis are needed to determine the minimal cost that satisfies system security.
The power market operations course has set guidelines to help make cost-effect and secure dispatch decisions for diverse system models. The final project for the course outlines a good practice problem of determining the least-cost dispatch for three generators, 5 transmission lines, phase shifters, and bidding segments. The problem definition will describe the project overview with given information and final expectations. The game plan will then be drawn to show how the author tackled the challenge. Program components are discussed to categorize the project portions into manageable sub-programming projects. Finally, the process flow shows a high-level procedure for the life of the program.
Problem Definition
The final project instructions dictated that a program is written to automatically formulate, compute, and solve the security-constrained unit commitment model.
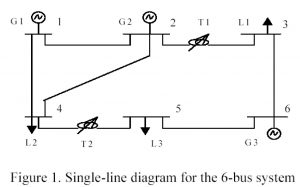
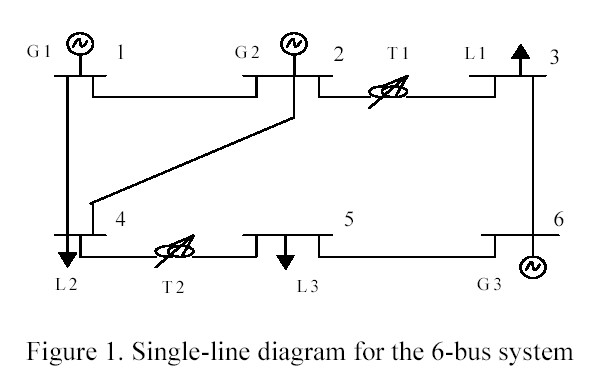
The testing system, a 6-bus system, depicted in Figure 1, has 3 units, 5 transmission lines, and 2 phase shifting transformers. System load and reserve requirements over the 24-hour horizon are shown in Table 1. Individual unit constraints are shown in Table 2. Unit bidding information is shown in Table 3. It is assumed that bidding for all the hours are the same. Variable startup cost information is shown in Table 4. Transmission line data are shown in Table 5. Phase shifting transformer data are shown in Table 6. Load distribution factors are shown in Table 7.




The consideration of phase-shifters and variable start-up costs was optional in the final project problem definition.
Game Plan
The approach on the project should have been at least a month before the due date to allow for plenty of time to tackle bugs in the program and formulations. The author’s approach was to tackle each subproblem of the unit commitment separately and combine the constraints and objective functions together into one master matrix to be processed by the MIP program. The project began determining a cost formulation for the test case generators. It was clear that the price of the generator would influence the formulation and the programming of the objective function and constraints. The formulation was done for every test case generator and a “variable-matrix” was formed to represent all the indicator variables, continuous variables, etc that the individual price and quantities formulated. Only the first few hours were used to test the program and generate constraints like the cost function for the generators. The author learned to develop algorithms to generate common patterns for NT (number of hours) hours. The start-up and shut-down indicators were formulated for the test case generators at any hour. Sample data was manually entered into excel from the formulations for the first test case generator and for the first few hours. The author then developed, after many long hours and failed attempts, loops to generate the correct matrices for hours 1:NT. The objective matrix, f, and the constraints, A, and Ae, were then exported from MATLAB using –ascii commands and then imported into excel. The output from the program was then compared against the expected output for the first few hours. “If”-else” statements, generated in excel, highlighted the programming output cells that deviated from the expected results. If the routines worked, they were added to the master program and the additional constraints were added to the master constraint matrix in the program. This process of write formulations, manually enter in first few hours test case generator 1, develop an algorithm, write code, test code, export output, and lastly compare the output to formulations continued for every subcomponent of the unit commitment.
Program Components
Unit Commitment
Cost Functions
For each test generator, there are bidding prices for each segment of MW generated. Segment prices can be either non-convex or convex. The prices are used in the objective function and it is desired to minimize these costs. The constraints for the formulations are also included.
Start-up and Shut-down indicators
These indicators represent the status of the generator, whether it is starting up or shutting down. Indicators are used for NT hours (24 hours in the case) and are useful in other formulations.
Start-up and Shut-down costs
Additional costs associated with the above start-up and shut-down indicators. It is the objective to minimize these costs throughout the system and throughout NT hours.
Capacities
Each test case generator has a minimum capacity it is willing to generate as being committed and a maximum capacity. These min and max limits are formulated as constraints for each generator for NT hours.
Reserves
The 10-minute spinning reserve of a unit is the unloaded synchronized generation that can ramp up in 10 minutes. The spinning reserve of a unit cannot exceed the difference between its maximum capacity and current generation. It is also limited by the 10-minute maximum sustained rate. Operating reserve is the unloaded synchronized/unsynchronized generating capacity that can ramp up in 10 minutes. When a unit is in operation, its operating reserve is the same as spinning reserve. When a unit is down, its operating reserve is the same as its quick start capability. These limits are represented as constraints with their respective indicator variables.
Ramping Constraints
From one hour to the next, a unit cannot increase its output above a maximum
increment, which is called the ramping up limit. Similarly, a unit cannot decrease its output above a maximum decrement, which is called the ramping down limit. These limits are represented as constraints with indicator variables.
Minimum uptime/downtime constraints
Minimum uptime constraint implies that a unit must stay in operation for a certain number of hours before it can be shut down; minimum downtime constraint implies that a unit must remain down for a certain number of hours before it can be brought online. Indicator variables can be used to represent these limits in the constraints.
System load balance and reserve requirements
These are constraints that the generators must meet the set load D, spinning reserve requirements, and operating reserve requirements. These constraints are also represented using indicator variables.
Variable Start-Up Costs
These costs were not considered in the project, however, they are time sensitive and depend on previous hour status.
Security
DC Power Flow
DC power flow is used as a quick solution to the test case system. The bus, load, and line data is entered into the program as arrays. The impedance matrices can be determined.
Power Transfer Distribution Factors
Based on the system bus, line, and load data, PTDF’s can be formulated for each bus 1-N, N-N, and then represented as constraints using indicator variables. Line flow and phase shifter limits must also be included.
Process Flow
Flow diagrams will illustrate some high-level processes for the program. The first diagram, Figure 2, shows the game plan process for each subcomponent.



Unit Commitment
This section of the final project for programming the SCUC will focus only on the unit commitment portion of the problem. The formulation section lists all relevant equations needed to form the unit commitment. The algorithms section discusses some techniques in generating the constraints or implementing the formulation into MATLAB. The appendix lists code referenced for unit commitment.
Formulation
Cost Functions
For a convex function the formulation is as follows:
Convex function

For a non-convex function, the formulation is as follows:
Non-Convex function

Table 3 (see above) represents the bidding segments and prices for the test case in the assignment. Table 2a (see above) represents the test case unit capacities and no-load costs.
G1 is non-convex, G2 is convex, G3 is convex
For G1 at any hour
c1,t = 200u1,t + 20px1,t,1 + 25px1,t,2 + 24px1,t,3 + 23px1,t,4
p1,t = px1,t,1 + px1,t,2 + px1,t,3 + px1,t,4
40δ1,t,1 ≤ px1,t,1 ≤ 40u1,t
60δ1,t,2 ≤ px1,t,2 ≤ 60δ1,t,2
80δ1,t,3 ≤ px1,t,3 ≤ 80δ1,t,3
0 ≤ px1,t,4 ≤ 40δ1,t,4
Objective Function Array
f =

Constraints Matrix
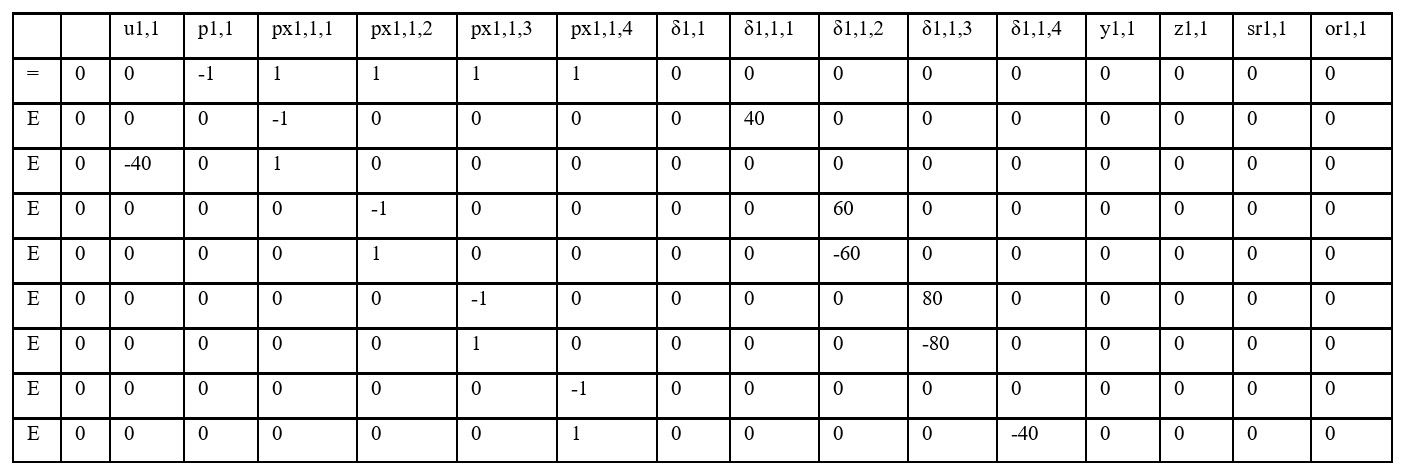
Bounds Arrays

For G2 at any hour
c2,t = 150u2,t + 24px2,t,1 + 26px2,t,2 + 28px2,t,3
p2,t = px2,t,1 + px2,t,2 + px2,t,3
0 ≤ px2,t,1 ≤ 30
0 ≤ px2,t,2 ≤ 50
0 ≤ px2,t,3 ≤ 20
Objective Function Array
f =

Constraints Array
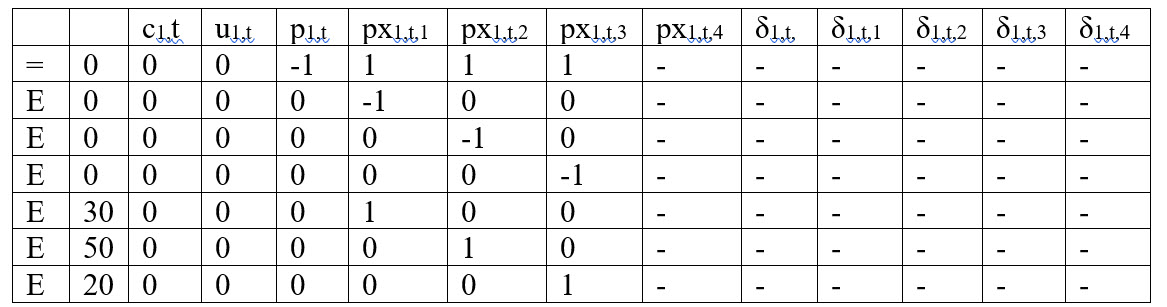
Bounds Arrays

For G3 at any hour
c3,t = 50u3,t + 30px3,t,1 + 32px3,t,2
p3,t = px3,t,1 + px3,t,2
0 ≤ px2,t,1 ≤ 10
0 ≤ px2,t,2 ≤ 20
Start-up and shut-down indicators
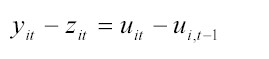
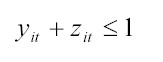
For G1 at any hour
y1,t – z1,t – u1,t + u1,(t-1) = 0
y1,t + z1,t ≤ 1
For G2 at any hour
y2,t – z2,t – u2,t + u2,(t-1) = 0
y2,t + z2,t ≤ 1
For GN at any hour
yN,t – zN,t – uN,t + uN,(t-1) = 0
yN,t + zN,t ≤ 1
Example for G1 for Hours 1 through 4
objective function array
f =

constraints matrix
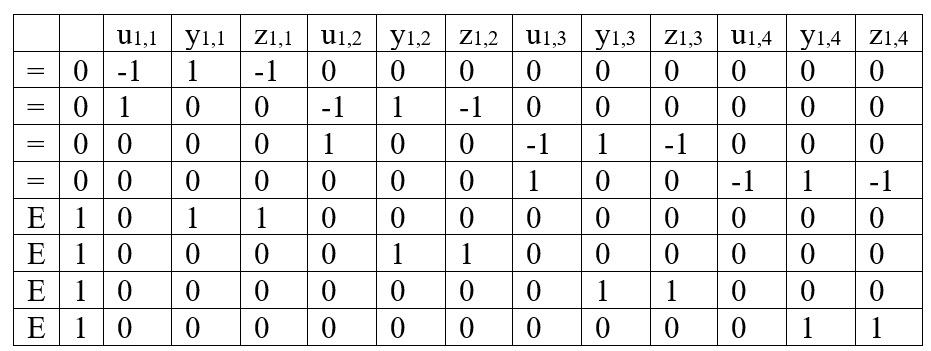
for hour 1
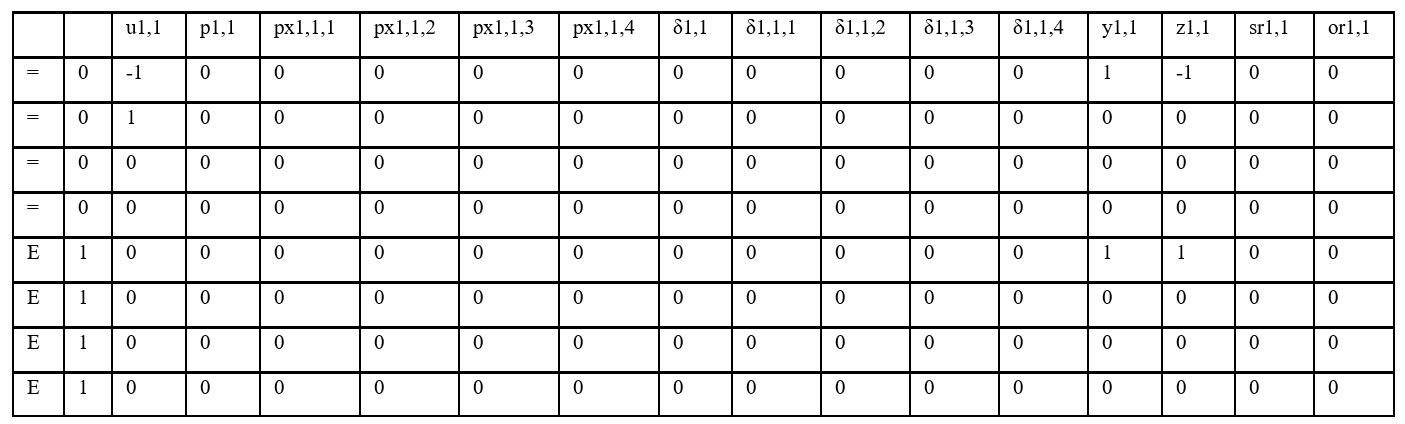
for hour 2
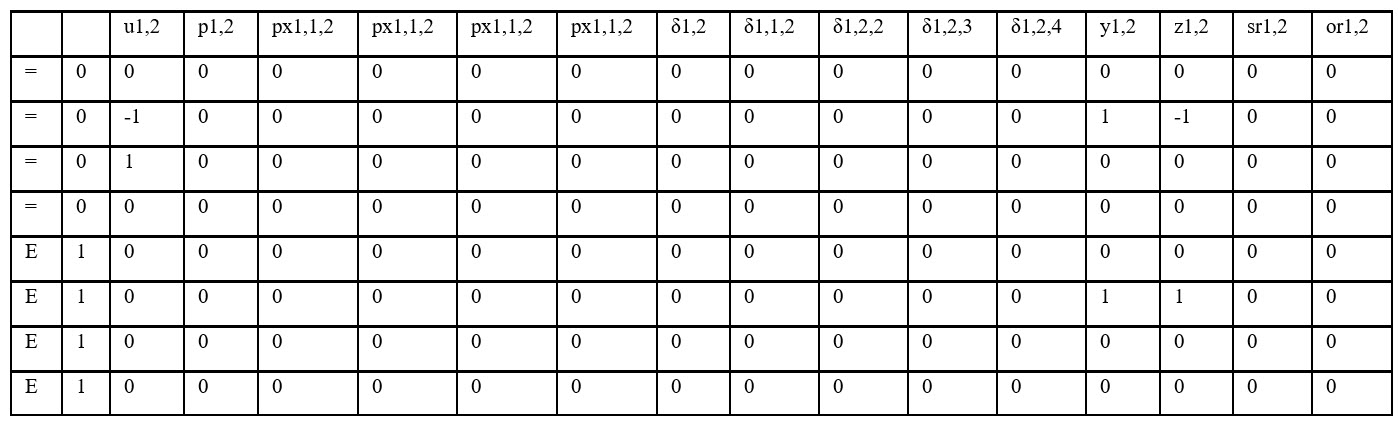
for hour 3
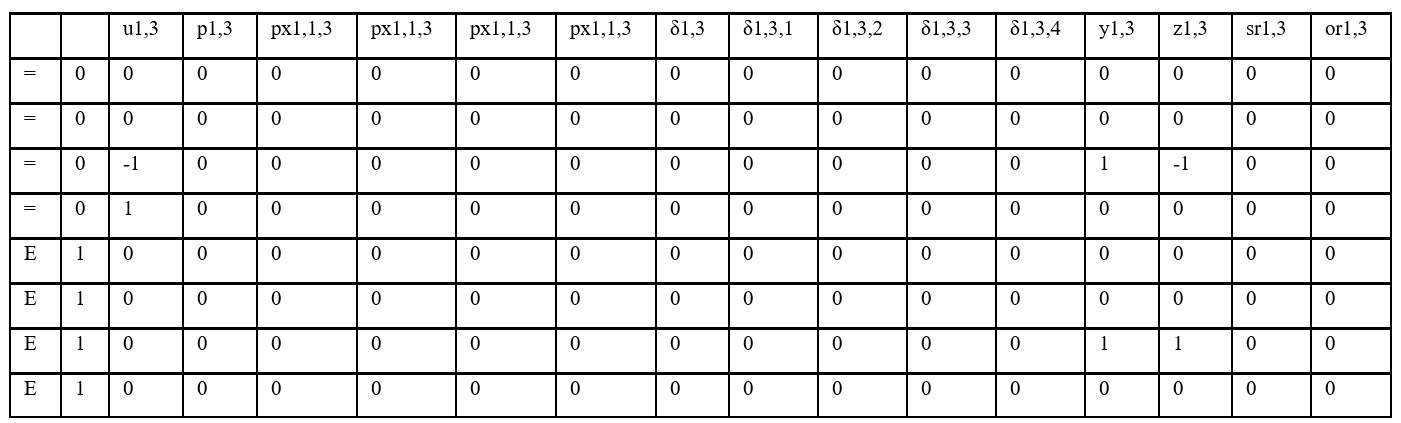
bounds array

Notes: The arrays will be the same pattern for each generator but the combined array will have variables representative of each generator for each hour
For a N Generator system with NT hours, there will be (3)X(N)X(NT) variables and (2)X(N)X(NT) rows. For the test case, 3 generators and 24 hours, there will be 216 variables to represent the start-up and shut-down indicators and 144 rows with constraints.
Combined Objective Function
f = [G1variables Hour1 G1 variables Hour 2 …. G1 variables Hour NT G2variables Hour1 G2 variables Hour 2 …. G2 variables Hour NT …. GNvariables Hour1 GN variables Hour 2 …. GN variables Hour NT]
Similar procedure as above can be applied to combine the equality and inequality constraints and upper, lower bounds, and integer array.
Download Report
The remainder of the project is discussed in a report downloadable from here:
Download “Security-Constrained Unit Commitment Programming Project” here
My Solution Code
You can view and download the GitHub repository here.
You can also download a zip archive of the project code here.