A Mixed-Integer Linear Programming (MILP) Problem for Generator Bids
The Challenge
Two generators (G1 and G2) are competing to supply a 60MW load. The bidding information of the two generators is shown in Table 1 for G1 and in Table 2 for G2. The minimum and maximum capacities for G1 are 15MW and 65MW, respectively. The minimum and maximum capacities for G2 are 10MW and 80MW, respectively.
Assume each unit has a no-load cost. No-load cost for G1 is $100. No-load cost for G2 is $200.
Bidding Tables
| Table 1. G1 Bidding Information | |
| Quantity (MW) | Price ($/MWh) |
| 20 | 20 |
| 30 | 25 |
| 15 | 30 |
| Table 2. G2 Bidding Information | |
| Quantity (MW) | Price ($/MWh) |
| 15 | 28 |
| 40 | 26 |
| 25 | 32 |
Deliverables
Find the minimum cost to supply the load and the accepted quantities for G1 and G2. Formulate the problem using mixed-integer linear programming.
- Complete MILP formulation (variables, objective function, constraints, bounds)
- Optimal solutions (commitment of units, accepted quantities, cost to supply the load)
Hints
- It’s possible that only one unit is needed to supply the load.
- If a unit is committed, a no-load cost will be incurred.
- Cost curve for G1 is convex when it’s committed. Cost curve for G2 is non-convex when it’s committed.
Formulation
Variables
There are 14 variables in my generator model problem: x1, x2, x3, x4, x5, x6, x7, x8,x9,x10,x11,x12,x13,x14. They are defined as given below:
| Variable | Definition |
| x1 | G1 Accepted Quantity 20 MW Step |
| x2 | G1 Accepted Quantity 30 MW Step |
| x3 | G1 Accepted Quantity 15 MW Step |
| x4 | G1 = x1 + x2 + x3 or total MW to be accepted by G1 |
| x5 | G2 Indicator Variable |
| x6 | G2 Indicator Variable |
| x7 | G2 Indicator Variable |
| x8 | G2 Indicator Variable |
| x9 | G2 Variable |
| x10 | G2 Variable |
| x11 | G2 Variable |
| x12 | G2 = x5 + x6 + x7 + x8 + x9 + x10 + x11 or total MW to be accepted by G2 |
| x13 | Unit commitment status of G1 |
| x14 | Unit commitment status of G2 |
Objective Function
The objective of the problem is to minimize cost of combined bids of both generators.
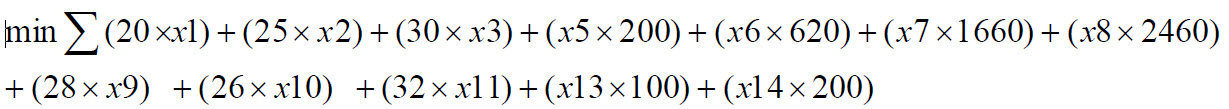
The objective function is the sum of the unit price of the MW multiplied by the quantity to be accepted added to the other ranges and their respective products plus the no-load cost.
Note: In the MATLAB portion of the model, the x4 and x12 variables are set equal to 0 since it is not in the problem definition to minimize these.
Constraints
The constraints of the problem are shown below:
Bounds
The bounds of the model are defined in the problem statement and are shown below:
| Variable | Lower Bound | Upper Bound |
| x1 | 0 | 20 |
| x2 | 0 | 30 |
| x3 | 0 | 15 |
| x4 | 15 | 65 |
| x5 | 0 | 1 |
| x6 | 0 | 1 |
| x7 | 0 | 1 |
| x8 | 0 | 1 |
| x9 | 0 | Inf |
| x10 | 0 | Inf |
| x11 | 0 | Inf |
| x12 | 10 | 80 |
| x13 | 0 | 1 |
| x14 | 0 | 1 |
MATLAB Setup
See the setup of the formulation in the MATLAB code here.
Solution
Optimal Solution
The accepted quantity from each generator range is shown below and in the MATLAB results:
| G1 Accepted Quantities Information | |
| Quantity (MW) | Price ($/MWH) |
| 20 | 20 |
| 30 | 25 |
| 10 | 30 |
| G2 Accepted Quantities Information | |
| Quantity (MW) | Price ($/MWH) |
| 0 | 28 |
| 0 | 26 |
| 0 | 32 |
Total Cost to Supply Load
Unit G2 is not committed, but G1 is committed with a total cost of:
20X20+30X25+10X30+100= $1550
The total minimized cost to supply load is $1550
Code
You may download a copy of the project by visiting the code repo here.
